[最も選択された] 三角形 面積 の 求め 方 小学生 311330

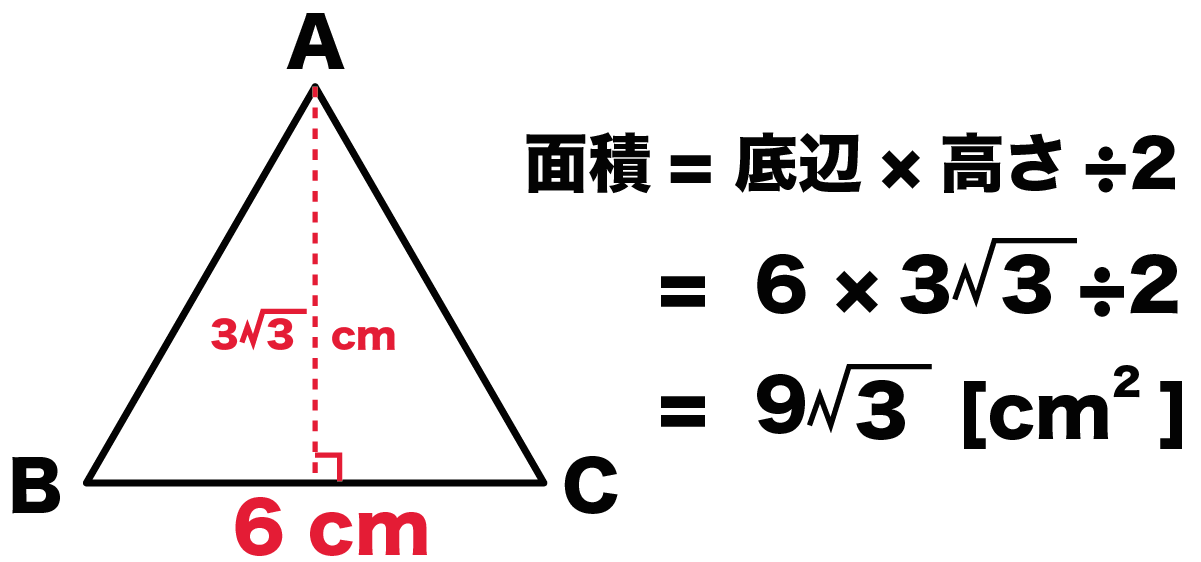
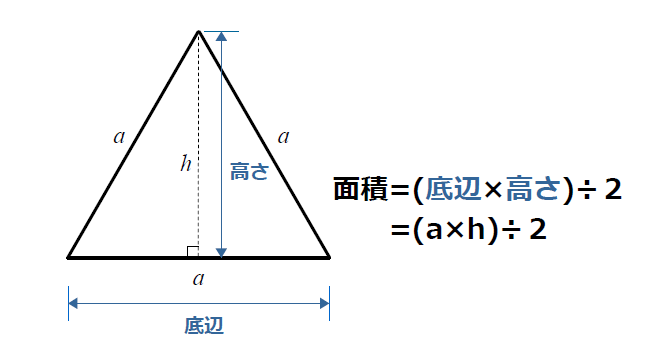
三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

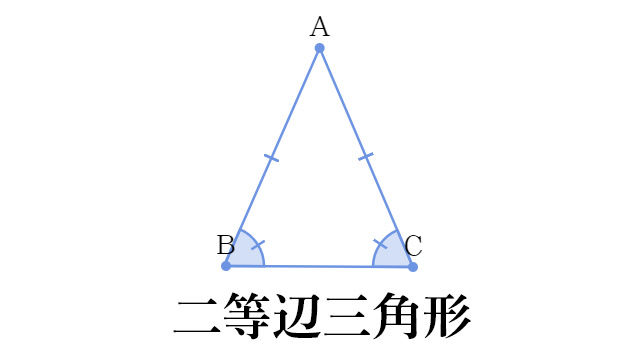
 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。 三角形の内角の和というのは，三角形の内側の角の大きさの和のことをいいます。 三角形の内角の和＝180° 小学生女の子 正三角形の1つの角の大きさが60°で角は3つだからピタゴラスの定理を使用する どのような直角三角形でも、斜辺の長さをc、他の二辺をa、bとしたときに、a 2 b 2 = c 2 が成り立つことがピタゴラスの定理で証明されています。 この定理を利用すると正三角形の高さを求められます。

三角形 面積 の 求め 方 小学生

三角形 面積 の 求め 方 小学生- ・正方形や円などの面積，直方体の体積の求め方を 黒板にまとめておくとよい。 ・様々な柱体と錐体を見せ，円柱，円錐など名称を 言わせる。 展 開 1 ②円柱と円錐，四 角柱と四角錐の 体積の関係から， 同じ底面積で同 じ高さをもつ他 の立体（五角柱と《三角柱の体積の求め方》 三角正方形・長方形の面積の求め方｜小学生に教えるための分かりやすい解説 管理人 9月 17, 18 / 11月 26, 18 それだけに、図形の面積の概念を学ぶ重要な単元です。

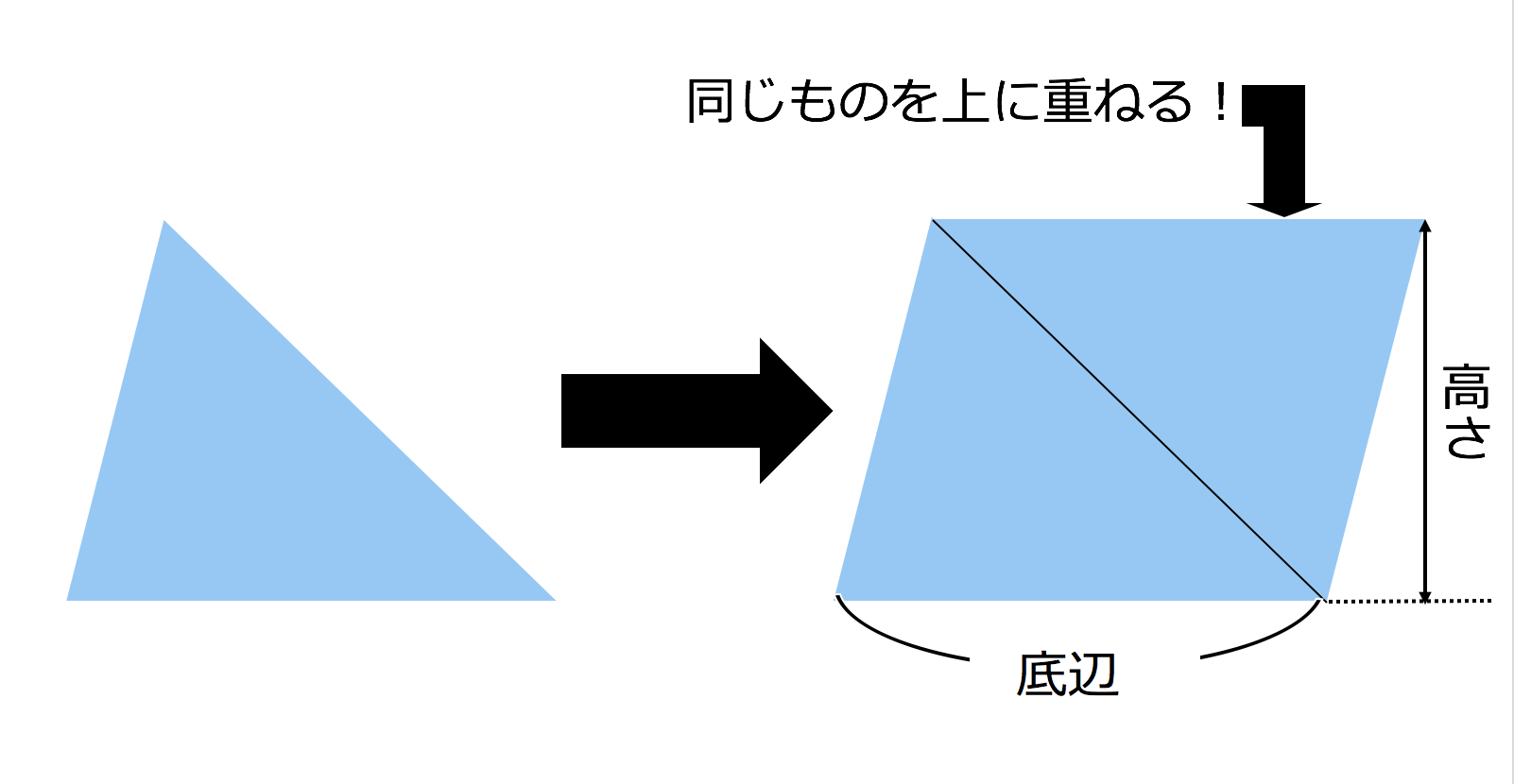
3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ

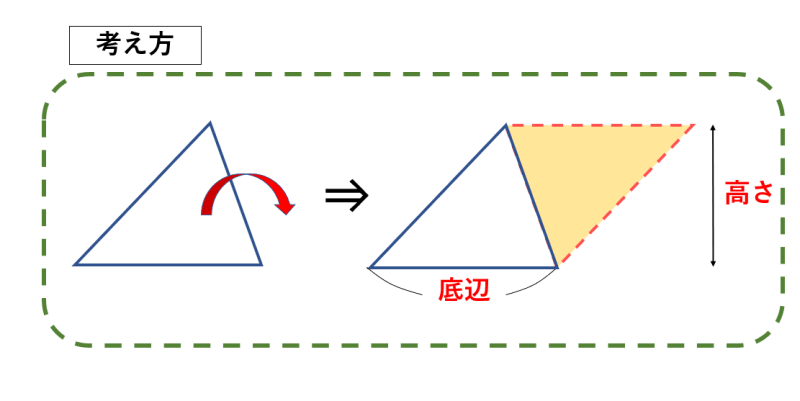
面積を求める 「ルーローの三角形」とは、運動学の父と呼ばれる19世紀ドイツの機械工学者フランツ・ルーローがつくり出した定幅図形である。 平面上のどの角度から見ても、幅 (径)が変わらない。 この図形の性質や使い途をご紹介し、関連する中学 どーも。猿田助です。 今日はやっと鈍角三角形の面積の求め方が分かったので、それについて書いていきたいと思います。 さて、皆さん。三角形の面積の求め方分かりますよね。 そうです。底辺 高さ÷2、です。 簡単ですよね。 では、なんでこの式で求められるかはわかりますか？面積比の求め方を理解しよう こちらの記事で説明したように、 三角形の面積比は「（底辺の比）×（高さの比）」 で求めます。 人によっては三角形だと納得しにくいかもしれませんが、例えば正方形であればノートのマス目などを見てわかりやすいと思います。

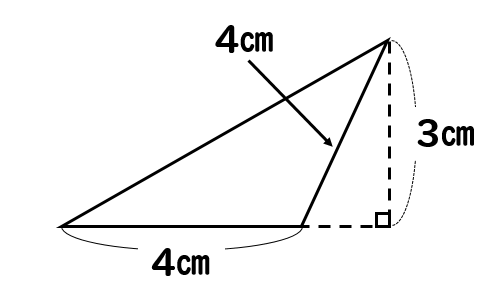
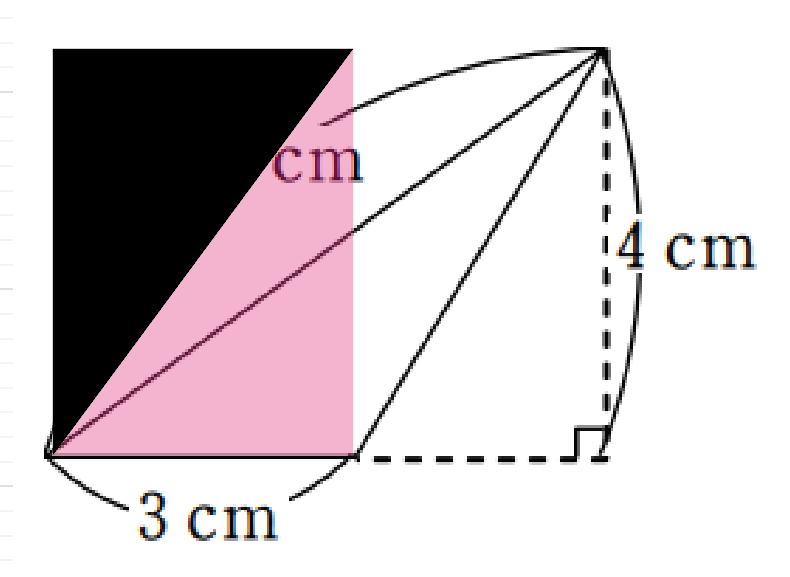
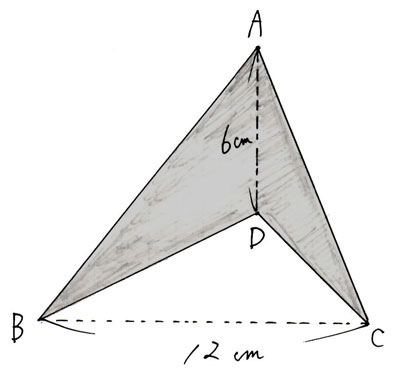
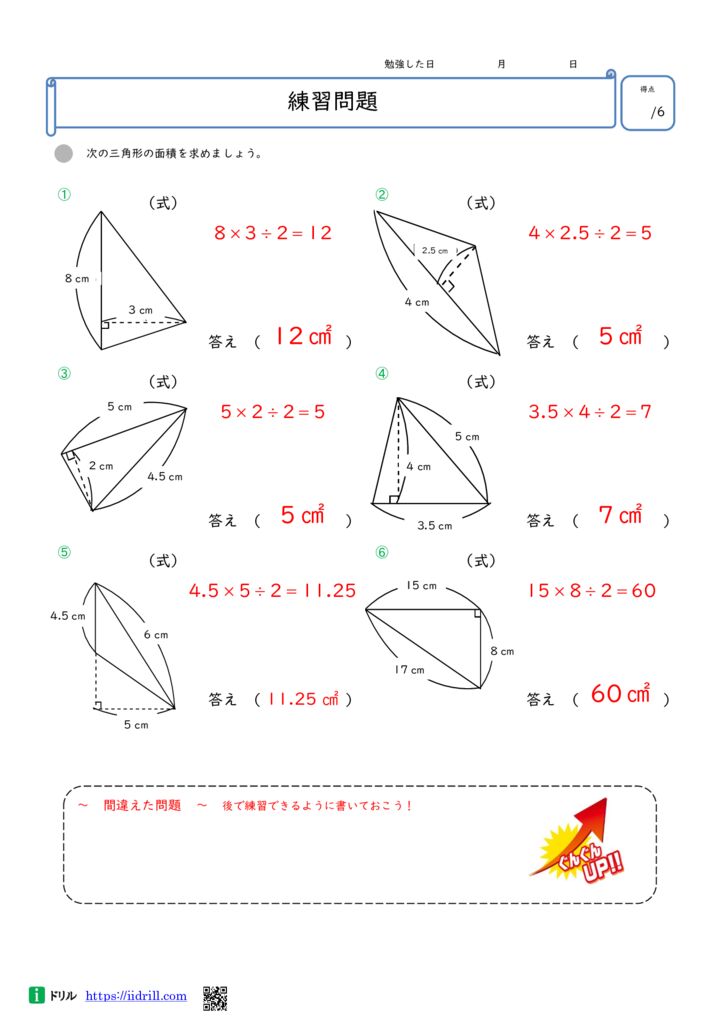
 今回のテーマである、手元の図面を使った、土地の面積の求め方は「三斜求積法」を使います。 簡単にいうと、土地の形状を複数の三角形に分割して面積を求める方法です。 ちょっと意味不明ですね。 以下でやり方の手順を詳しく解説します。 小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむす 角度の求め方 算数の教え上手 学びの場 Com 余弦定理で角度を求める方法 数学の星 小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむす 中学数学 正三角形の角度の求め方が 高さのわからない三角形の面積の求め方を教えてください。 問題は画像の通りです。 角度はわかりません。 ちなみに答えは 辺をacを底辺として8×3÷2＝12㎠ と新聞にありました。 この答 えにたどりつく過程を教えてください。

三角形 面積 の 求め 方 小学生のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

3	3	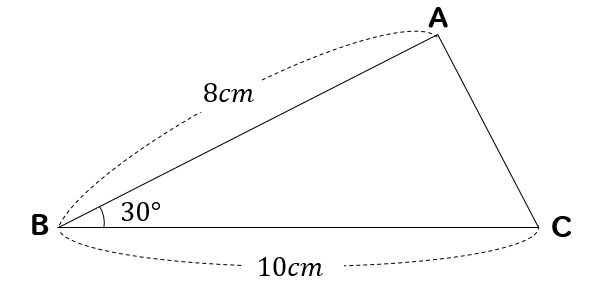3
3	3	3
3	3	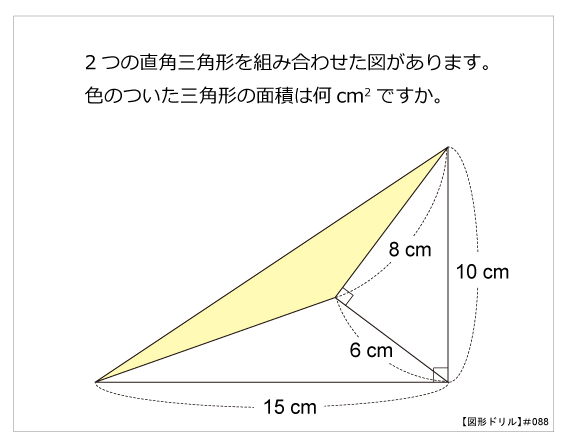3
3	3	3
3	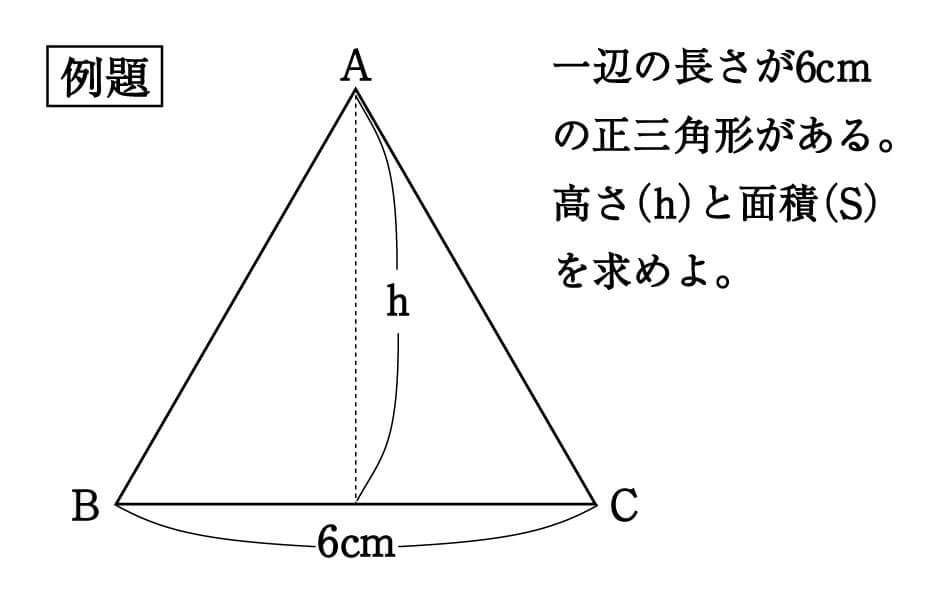3	3
3	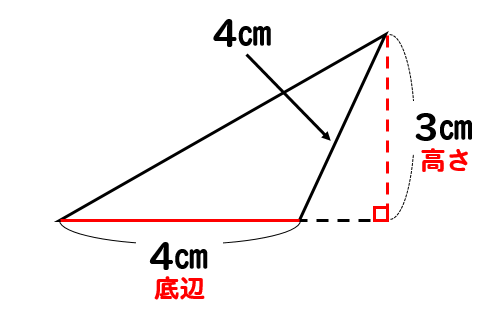3	3
3	3	3
3	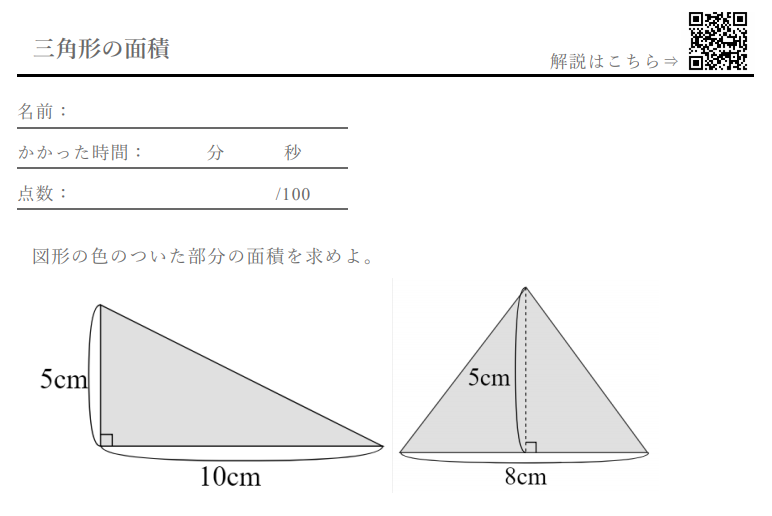3	3
3	3	3
3	3	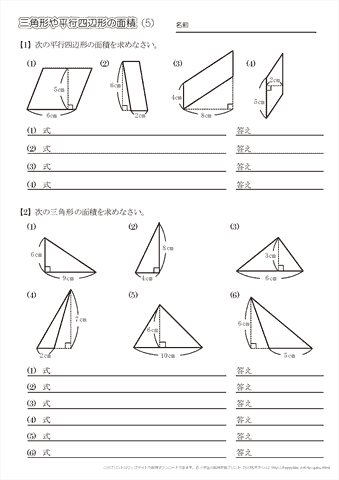3
3	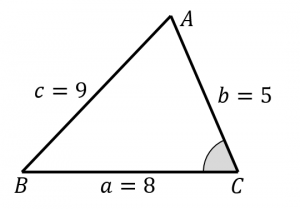3	3
3	3	3
3	3	3
3	3	3
3	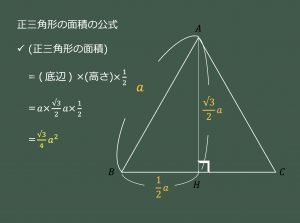3	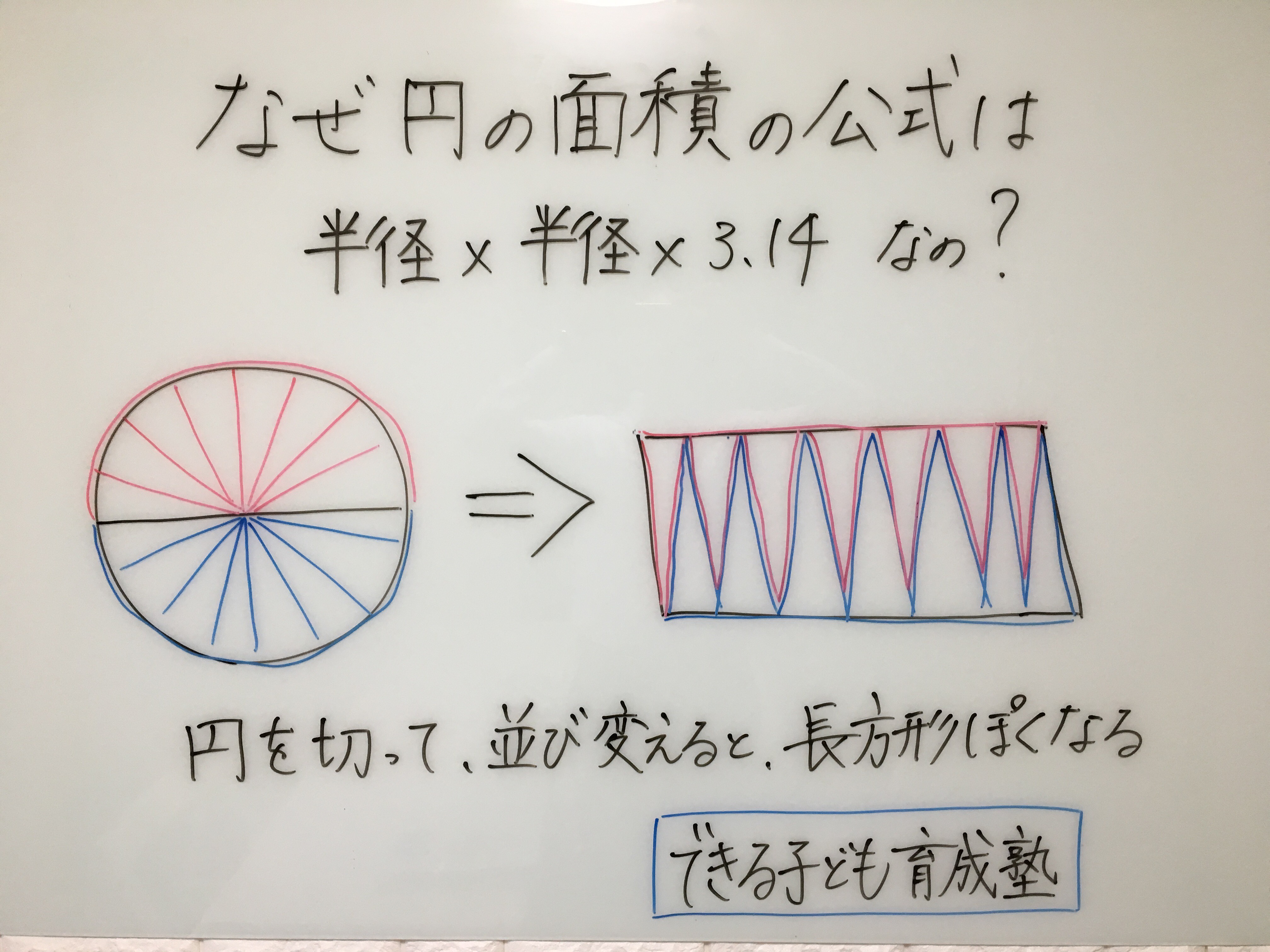3
3	3	3
3	3	3
3	3	3
3	3	3
3	3	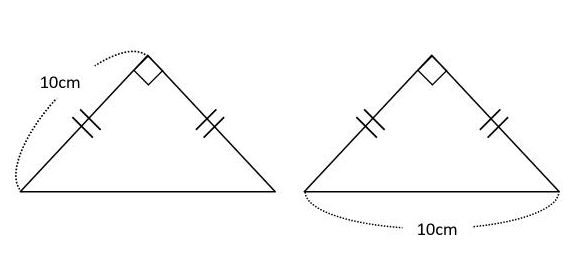3
3	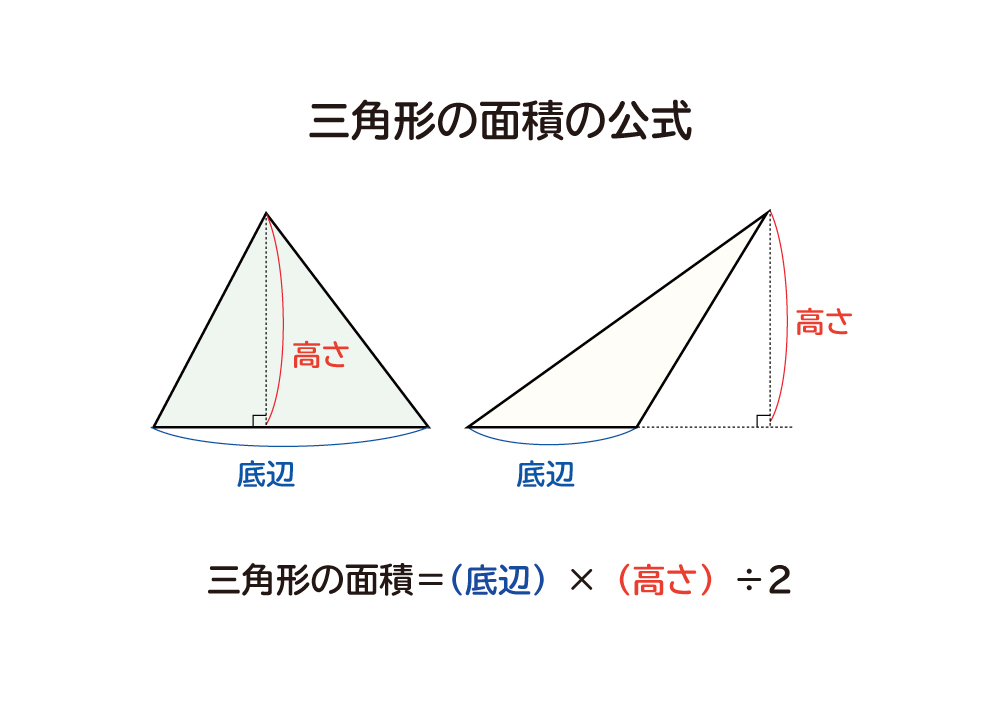3	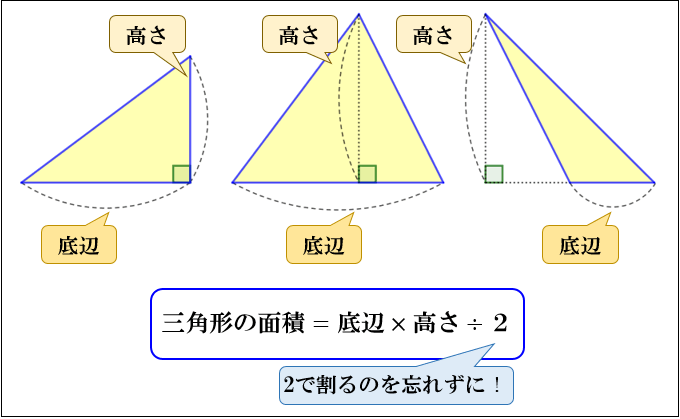3
3	3	3
3	3	3
3	3	3
3	3	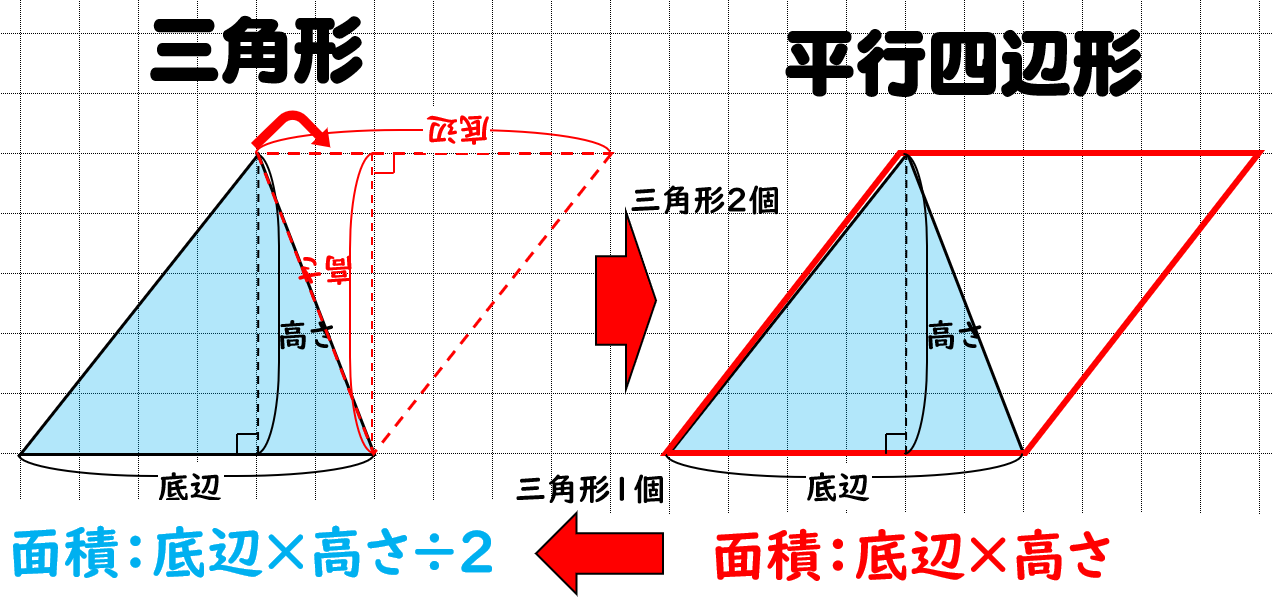3
3	3	3
3	3	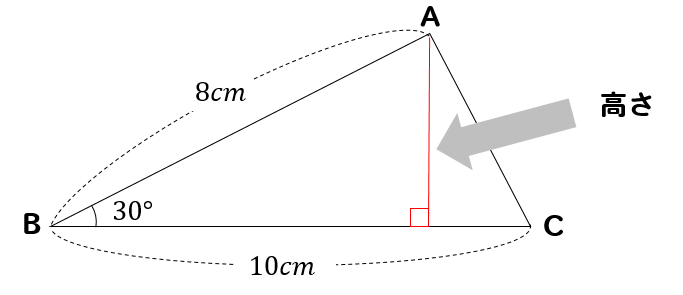3
3	3	3
3	3	3
3	3	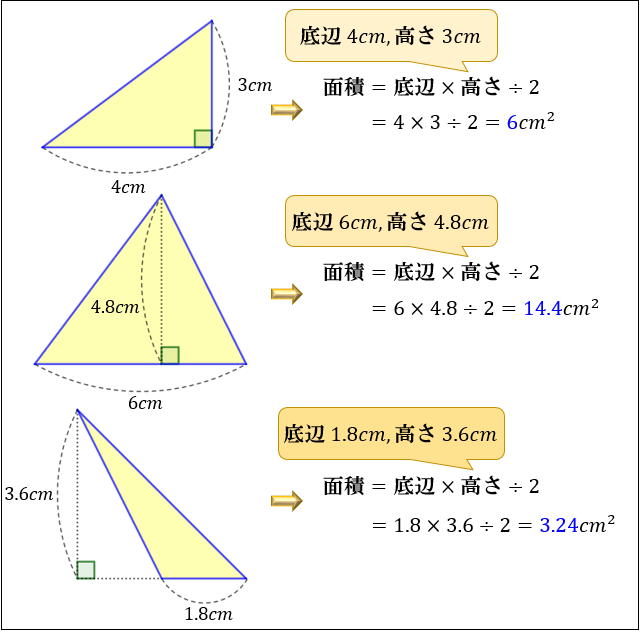3
3	3	3
3	3	3
3	3	3
3	3	3
3	3

 四角錐の表面積＝底面積＋側面積 で求めることができますが この段階でわかっているのは底面積＝6×6＝36（cm²）ということだけです。 側面の三角形の面積がわからないと全体の表面積を求めることができないので、側面の三角形の面積を求めなくては小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題